Congruency of Shapes

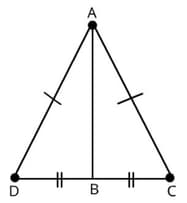
The two triangles made by the diagonal of a parallelogram are always congruent to each other. Prove it

Look at the rotations in the two figures and answer the questions below separately for each:

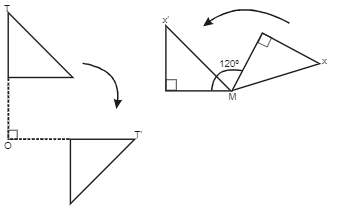
Direction of rotation? (clockwise/anti-clockwise)

Look at the rotations in the two figures and answer the questions below separately for each:

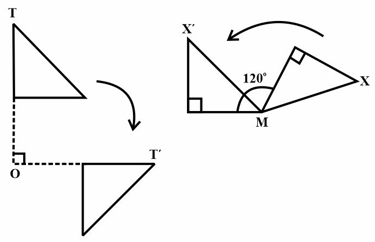
The point of rotation is _____.

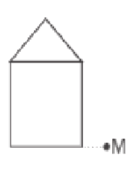
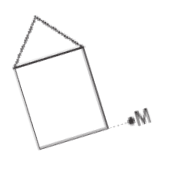
Taking point $\text{'}\mathrm{M}\text{'}$ to be the point of rotation, rotate the following figure anticlockwise by $30°$ of above image is 

The symbol $\cong$ is used to represent _____ triangles.

If $AB=DF, AC=DE \& BE=FC$ then prove that $△ABC\cong △DFE$.

These shapes are congruent.

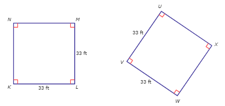
Which of the following figures are congruent to the square $ABCD$.

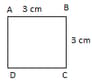
How can two squares have the same angles but not be congruent?

Two squares are congruent if both of them have the same length of the _____.

P is the midpoint of a line segment MN. If MP = 5 cm, find the length of PN.

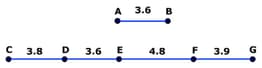
$ \overline{\text{AB}}$ and $ \overline{\text{CG}}$ are two line segments whose lengths are given in cms. The line segment $ \overline{\text{CG}}$ is divided into different segments.

$ \overline{\text{AB}}$≅

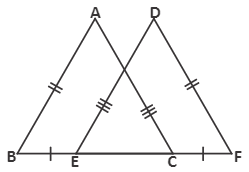
In the triangle ADC, which line segment is $ \overline{\text{AD}}$ congruent to ?

Length of the line segment $ \overline{\text{AC}}$ is 8 cm. B is the midpoint of the line segment. The length of $ \overline{\text{AB}}$ is

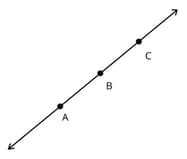
How many line segments are possible using 3 points in a line, where any two of the points are end points?

The maximum number of line segments that can be drawn using 3 points with any two of the points as end points is

The number of line segments that can be drawn through two points M and N is

The number of line segments that can be drawn through the point A is